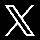Leonhard Euler
| ||||||||||||
Leonhard Euler. Reconocido matemático y físico. Considerado el principal matemático del Siglo XVIII y uno de los más grandes de todos los tiempos.
Vivió en Rusia y Alemania la mayor parte de su vida y realizó importantes descubrimientos en áreas tan diversas como el cálculo o la Teoría de grafos.
Introdujo gran parte de la moderna terminología y notación matemática, particularmente para el área del Análisis matemático, como por ejemplo la noción de función matemática. Asimismo se le conoce por sus trabajos en los campos de la mecánica, óptica y astronomía.
Sumario
Vida
Primeros años
Leonhard Paul Euler nació el 15 de abril de 1707 en Basilea, Suiza hijo de Paul Euler, un pastor calvinista, y de Marguerite Brucker, hija de otro pastor. Tuvo dos hermanas pequeñas llamadas Anna Maria y Maria Magdalena. Poco después de su nacimiento, su familia se trasladó de Basilea a la ciudad de Riehen, en donde Euler pasó su infancia. Por su parte, Paul Euler era amigo de la familia Bernoulli, famosa familia de matemáticos entre los que destacaba Johann Bernoulli, que en ese momento era ya considerado el principal matemático europeo, y que ejercería una gran influencia sobre el joven Leonhard.
La educación formal de Euler comenzó en la ciudad de Basilea, donde le enviaron a vivir con su abuela materna. A la edad de 13 años se matriculó en la Universidad de Basilea, y en 1723 recibiría el título de maestro de Filosofía tras una disertación comparativa de las filosofías de René Descartes e Isaac Newton. Por entonces, Euler recibía lecciones particulares de Johann Bernoulli todos los sábados por la tarde, quien descubrió rápidamente el increíble talento de su nuevo pupilo para las matemáticas.
En aquella época Euler se dedicaba a estudiar teología, griego y hebreo siguiendo los deseos de su padre, y con la vista puesta en llegar a ser también pastor. Johann Bernoulli intervino para convencer a Paul Euler de que Leonhard estaba destinado a ser un gran matemático.
En 1726 Euler finalizó su Doctorado con una tesis sobre la propagación del sonido bajo el título "De Sono" y en 1727 participó en el concurso promovido por la Academia de las Ciencias francesa por el cual se solicitaba a los concursantes que encontraran la mejor forma posible de ubicar el mástil en un buque. Ganó el segundo puesto, detrás de Pierre Bouguer, que es conocido por ser el padre de la arquitectura naval. Más adelante Euler conseguiría ganar ese premio hasta en doce ocasiones.
En San Petersburgo
Por aquella época, los dos hijos de Johann Bernoulli, Daniel y Nicolás, se encontraban trabajando en la Academia de las ciencias de Rusia en San Petersburgo.
En Julio de 1726, Nicolás murió de apendicitis tras haber vivido un año en Rusia y, cuando Daniel asumió el cargo de su hermano en el departamento de matemáticas y física, recomendó que el puesto que había dejado vacante en fisiología fuese ocupado por su amigo Euler.
En noviembre de ese mismo año Euler aceptó la oferta, aunque retrasó su salida hacia San Petersburgo mientras intentaba conseguir, sin éxito, un puesto de profesor de física en la Universidad de Basilea. Euler llegó a la capital rusa el 17 de mayo de 1727. Fue ascendido desde su puesto en el departamento médico de la Academia a un puesto en el departamento de matemáticas, en el que trabajó con Daniel Bernoulli, a menudo en estrecha colaboración. Euler aprendió el ruso y se estableció finalmente en San Petersburgo a vivir. Llegó incluso a tomar un trabajo adicional como médico de la Armada de Rusia.
La Academia de San Petersburgo, creada por Pedro I de Rusia, tenía el objetivo de mejorar el nivel educativo en Rusia y de reducir la diferencia científica existente entre ese país y la Europa Occidental. Como resultado, se implementaron una serie de medidas para atraer a eruditos extranjeros como Euler. La Academia poseía amplios recursos financieros y una biblioteca muy extensa, extraída directamente de las bibliotecas privadas de Pedro I y de la nobleza. La Academia admitía a un número muy reducido de estudiantes para facilitar la labor de enseñanza, a la vez que se enfatizaba la labor de investigación y se ofrecía a la facultad tanto el tiempo como la libertad para resolver cuestiones científicas.
Sin embargo, la principal benefactora de la Academia, la emperatriz Catalina I de Rusia, que había continuado con las políticas progresistas de su marido, murió el mismo día de la llegada de Euler a Rusia. Su muerte incrementó el poder de la nobleza, puesto que el nuevo emperador pasó a ser Pedro II de Rusia, por entonces un niño de tan sólo 12 años de edad. La nobleza sospechaba de los científicos extranjeros de la Academia, por lo que cortó la cuantía de recursos dedicados a la misma y provocó otra serie de dificultades para Euler y sus colegas.
Las condiciones mejoraron ligeramente tras la muerte de Pedro II, y Euler fue poco a poco ascendiendo en la jerarquía de la Academia, convirtiéndose en profesor de física en 1731. Dos años más tarde, Daniel Bernoulli, harto de las dificultades que le planteaban la censura y la hostilidad a la que se enfrentaban en San Petersburgo, dejó la ciudad y volvió a Basilea. Euler le sucedió como director del departamento de matemáticas.
El 7 de enero de 1734 Euler contrajo matrimonio con Katharina Gsell, hija de un pintor de la Academia. La joven pareja compró una casa al lado del río Neva y llegó a concebir hasta trece hijos, si bien sólo cinco sobrevivieron hasta la edad adulta.
Berlín
Preocupado por los acontecimientos políticos que estaban teniendo lugar en Rusia, Euler partió de San Petersburgo el 19 de junio de 1741 para aceptar un cargo en la Academia de Berlín, cargo que le había sido ofrecido por Federico II el Grande, rey de Prusia. Vivió veinticinco años en Berlín, en donde escribió más de 380 artículos. También publicó aquí dos de sus principales obras: la Introductio in analysin infinitorum, un texto sobre las funciones matemáticas, publicado en 1748, y la Institutiones calculi differentialis, publicada en 1755 y que versaba sobre el Cálculo diferencial.
Además, se le ofreció a Euler un puesto como tutor de la princesa de Anhalt-Dessau, la sobrina de Federico. Euler escribió más de 200 cartas dirigidas a la princesa que más tarde serían recopiladas en un volumen titulado Cartas de Euler sobre distintos temas de Filosofía Natural dirigidas a una Princesa Alemana. Este trabajo recopilaba la exposición de Euler sobre varios temas de físicas y matemáticas, así como una visión de su personalidad y de sus creencias religiosas. El libro se convirtió en el más leído de todas sus obras, y fue publicado a lo largo y ancho del continente europeo y en los Estados Unidos. La popularidad que llegaron a alcanzar estas Cartas sirve de testimonio sobre la habilidad de Euler de comunicar cuestiones científicas a una audiencia menos cualificada.
Sin embargo, y a pesar de la inmensa contribución de Euler al prestigio de la Academia, fue obligado finalmente a dejar Berlín. El motivo de esto fue, en parte, un conflicto de personalidad entre el matemático y el propio Federico, que llegó a ver a Euler como una persona muy poco sofisticada, y especialmente en comparación con el círculo de filósofos que el rey alemán había logrado congregar en la Academia. Voltaire, en particular, era uno de esos filósofos, y gozaba de una posición preeminente en el círculo social del rey. Euler, como un simple hombre de carácter religioso y trabajador, era muy convencional en sus creencias y en sus gustos, representando en cierta forma lo contrario que Voltaire. Euler tenía conocimientos limitados de Retórica, y solía debatir cuestiones sobre las que tenía pocos conocimientos, lo cual le hacía un objetivo frecuente de los ataques del filósofo. Por ejemplo, Euler protagonizó varias discusiones metafísicas con Voltaire, de las que solía retirarse enfurecido por su incapacidad en la Retórica y la metafísica. Federico también mostró su descontento con las habilidades prácticas de ingeniería de Euler.
Deterioro de la visión
La vista de Euler fue empeorando a lo largo de su vida. En el año 1735 Euler sufrió una fiebre casi fatal, y tres años después de dicho acontecimiento quedó casi ciego de su ojo derecho. Euler, sin embargo, prefería acusar de este hecho al trabajo de Cartografía que realizaba para la Academia de San Petersburgo.
La vista de ese ojo empeoró a lo largo de su estancia en Alemania, hasta el punto de que Federico hacía referencia a él como el Cíclope. Euler más tarde sufrió Cataratas en su ojo sano, el izquierdo, lo que le dejó prácticamente ciego pocas semanas después de su diagnóstico. A pesar de ello, parece que sus problemas de visión no afectaron a su productividad intelectual, dado que lo compensó con su gran capacidad de cálculo mental y su memoria fotográfica. Por ejemplo, Euler era capaz de repetir la Eneida de Virgilio desde el comienzo hasta el final y sin dudar en ningún momento, y en cada página de la edición era capaz de indicar qué línea era la primera y cuál era la última. También se sabía de memoria las fórmulas de trigonometría y las primeras 6 potencias de los primeros 100 números primos.
Pasó los últimos años de su vida ciego, pero siguió trabajando. Muchos trabajos se los dictó a su hijo mayor.
Retorno a Rusia y Muerte
La situación en Rusia había mejorado enormemente tras el ascenso de Catalina la Grande, por lo que en 1766 Euler aceptó una invitación para volver a la Academia de San Petersburgo para pasar ahí el resto de su vida. Su segunda época en Rusia, sin embargo, estuvo marcada por la tragedia: un incendio en San Petersburgo en 1771 le costó su casa y casi su vida, y en 1773 perdió a su esposa, que por entonces tenía 40 años de edad. Euler se volvió a casar tres años más tarde.
El 18 de septiembre de 1783 Euler falleció en la ciudad de San Petersburgo tras sufrir un Accidente cerebrovascular, y fue enterrado junto con su esposa en el Cementerio Luterano ubicado en la Isla de Vasilievsky. Hoy en día el cementerio en el que fue enterrado Euler no existe, dado que fue destruido por los soviéticos. Éstos trasladaron previamente sus restos al monasterio ortodoxo de Alejandro Nevski.
Por su parte, Nikolaus von Fuss, ahijado de Euler y secretario de la Academia Imperial de San Petersburgo, escribió un relato de su vida junto con un listado de sus obras.
Líneas de trabajo
Los trabajos científicos de Euler abarcan prácticamente todas las matemáticas contemporáneas a él. En todas las ramas de las matemáticas hizo descubrimientos notables, que lo situaron en el primer lugar en el mundo. Euler fue capaz de comprender las matemáticas como un todo único, aunque enorme en el confluían un montón de ramas importantes y ante todo el Análisis. Laplace indicó que Euler fue el maestro común de todos los matemáticos de la segunda mitad del siglo XVIII.
La actividad de Euler, en lo fundamental tuvo una orientación algorítmica. A la construción de la teoría general llegaba partiendo de problemas concretos, los cuales tenían importancia práctica. En su herencia científica la práctica tiene un peso específico excepcionalmente grande. Aproximadamente el 40% de sus trabajos están dedicados a la matemática aplicada, la física, la mecánica, la hidromecánica, la teoría de la elasticidad, la balística, la construcción naval, la teoría de máquinas, la óptica y otras. Los rasgos algorítmicos son propios aún de sus trabajos de apariencia puramente teórica. Particularmente esto se advierte en los trabajos sobre análisis infinitesimal, el cual en esencia se construye como el aparato matemático de la mecánica clásica y la física.
Desde 1727 hasta 1783 la pluma de Euler no había cesado de extender las fronteras de prácticamente todas las ramas tanto e la matemática pura como aplicada, desde los niveles más elementales a los más avanzados. Además, Euler escribía casi siempre utilizando el lenguaje y las notaciones que aún usamos hoy, pues ningún otro matemático contribuyó en tal medida como él a dar su forma actual a la matemática que hoy llamamos clásica, siendo el más feliz inventor de notaciones de toda la historia de la matemática. A su llegada a San Petersburgo en 1727 se vio encargado de ciertos experimentos relativos al disparo de cañones, y en la exposición manuscrita de los resultados obtenidos, escrita probablemente en 1727 ó 1728, Euler utilizaba ya la letra e más de una docena de veces para representar la base del sistema de logaritmos naturales. La idea que representa este número había sido bien conocida prácticamente desde que se inventaron los logaritmos más de un siglo antes, y, sin embargo, no se había introducido ninguna notación estándar para representarlo.
En una carta a Goldbach de 1731, Euler vuelve a utilizar su letra e para "el número cuyo logaritmo hiperbólico es igual a 1"; esta notación apareció impresa por primera vez en la Mechanica de Euler, publicada en 1736, obra en la que se presenta por primera vez la mecánica newtoniana en forma analítica. Este símbolo, que quizá le vino sugerido a Euler por la primera letra de la palabra "exponencial", no tardó en ser admitido universalmente. La consagración definitiva del uso de la letra griega pi para representar la razón de la longitud de la circunferencia al diámetro, se debe también en buena medida a Euler, aunque ya se había utilizado en 1706, un año antes del nacimiento de Euler, en la Synopsis Palmoriorum Matheseos, o "Nueva introducción a la matemática" por William Jones (1675-1749). Fue, sin embargo, la adopción del símbolo por Euler, en 1737 en primer lugar, y después en sus popularísimos textos, lo que extendió su uso universalmente. El símbolo i para la raíz cuadrada de -1 es otra de las notaciones introducidas por Euler por primera vez, aunque en este caso lo adoptó hacia finales de su vida, en 1777. Probablemente este retraso se deba a que en sus obras anteriores había utilizado la letra i de una manera bastante sistemática para representar un "número infinito", en un sentido análogo pero no análogo al del i de Wallis.
De hecho Euler utilizó i para la raíz cuadrada de -1 en un manuscrito fechado en 1777, tal manuscrito no se publicó hasta 1794, de manera que fue la adopción de dicho símbolo por Gauss en su obra clásica Disuisitiones arithmeticae, de 1808, la que le aseguró un puesto definitivo en la historia de las notaciones matemáticas. Los símbolos e, e i de los que Euler fue en gran medida responsable, como hemos visto se relacionan con los dos enteros más importantes, 0 y 1, por medio de la famosa igualdad ei + 1= 0 en la que figuran los cuatro números más importantes y las más importantes operaciones y la relación de toda la matemática. Lo equivalente a esta igualdad, en forma generalizada, aparecen el más famoso de todos los textos de Euler, la Introductio in analysin infinitorum, publicado en 1748, pero el nombre de Euler no aparece hoy asociado a ninguno de los símbolos que intervienen en esta relación, sino que la llamada "constante de Euler", la que recibe este honor y se la considera una sexta constante matemática importante.
No sólo se utilizan hoy las notaciones introducidas por Euler para designar números importantes. También en geometría, en álgebra, en trigonometría y en análisis nos encontramos a cada momento con el uso de los símbolos, terminología e ideas debidas a Euler. El uso de las letras minúsculas a, b, c, para los lados de un triángulo y de las correspondientes letras mayúsculas A, B, C, para los ángulos respectivamente opuestos a ellos, proviene de Euler. La notación lx para el logaritmo de x, el uso tan familiar hoy de la sigma para representar una suma y, quizá la más importante de todas, la notación f(x) para una función de x, utilizada en los Commentarii de San Petersburgo de 1734-1735, son otras de las notaciones de Euler que seguimos utilizando en la actualidad. Se puede afirmar, pues, sin ninguna duda, que nuestro sistema de notaciones matemáticas es hoy lo que es debido más a Euler que a ningún otro matemático a lo largo de la historia.
Véase también
- Georg Simon Ohm
- Joseph Louis Lagrange
- Matemáticas
- Legendre Adrien Marie
- Daniel Bernoulli
- Siméon Denis Poisson
- Familia Bernoulli
Enlaces externos
- The Euler Archive
- Lettres à une Princesse d'Allemagne
- Artículo en la Encyclopedia Britannica
- How Euler did it Página web que contiene explicaciones sobre cómo Euler resolvió diversos problemas.
- Euler Archive
- Euler Committee of the Swiss Academy of Sciences
- Tricentenario de Euler (año 2007)
- The Euler Society
- Leonhard Euler Congress 2007 — San Petrersburgo, Rusia.
- "Euler - 300th anniversary lecture", discurso pronunciado por Robin Wilson en Gresham College, el 9 mayo de 2007.
- Project Euler
- Árbol de familia de Euler