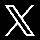Campana de Gauss
| ||||
Campana de Gauss , es una representación gráfica de la distribución normal de un grupo de datos. Éstos se reparten en valores bajos, medios y altos, creando un gráfico de forma acampanada y simétrica con respecto a un determinado parámetro. Se conoce como curva o campana de Gauss o distribución Normal.
Historia
Aunque la campana de Gauss lleva el nombre del genio de las matemáticas Carl Friedrich Gauss , realmente la distribución normal la descubrió y publico por primera vez Abraham Moivre (por eso en algunos libros se llama la distribución de Moivre – Gauss) en un artículo del año 1733, que reprodujo en la segunda edición de su obra “The Doctrine of Chance” (1738) como aproximación de la distribución normal para valores grandes de n. Este resultado fue ampliado por Pierre-Simon de Laplace en su libro “Teoría analítica de las probabilidades” (1812).
El nombre de Gauss se ha asociado a esta distribución porque la usó con profusión cuando analizaba datos astronómicos y algunos autores le atribuyen un descubrimiento independiente del de De Moivre.
El nombre de "campana" se lo dio Esprit Jouffret que uso este término (bell surface) (superficie campana) por primera vez en 1872.
Ecuaciones
La campana de Gauss está definida por la función:
Propiedades
- El campo de existencia es cualquier valor real, es decir, (-∞, +∞).
- Es simétrica respecto a la media µ.
- Tiene un máximo en la media µ.
- Crece hasta la media µ y decrece a partir de ella.
- En los puntos µ − σ y µ + σ presenta puntos de inflexión.
- El eje de abscisas es una asíntota de la curva.
- El área del recinto determinado por la función y el eje de abscisas es igual a la unidad.
- Al ser simétrica respecto al eje que pasa por x = µ, deja un área igual a 0.5 a la izquierda y otra igual a 0.5 a la derecha.
- La probabilidad equivale al área encerrada bajo la curva.
p(μ - σ < X ≤ μ + σ) = 0.6826 = 68.26 %
p(μ - 2σ < X ≤ μ + 2σ) = 0.954 = 95.4 %
p(μ - 3σ < X ≤ μ + 3σ) = 0.997 = 99.7 %
Aplicaciones
Una de las mayores aportaciones al cálculo integral que realizó Gauss, fue la introducción de esta función. Este gráfico se usa en variables asociadas a fenómenos naturales que siguen el modelo de la normal.
- Caracteres morfológicos de individuos (personas, animales, plantas,...) de una especie, p.ejm. tallas, pesos, envergaduras, diámetros, perímetros,...
- Caracteres fisiológicos, por ejemplo: efecto de una misma dosis de un fármaco, o de una misma cantidad de abono.
- Caracteres sociológicos, por ejemplo: consumo de cierto producto por un mismo grupo de individuos, puntuaciones de examen.
- Caracteres [Psicología|psicológicos]], por ejemplo: cociente intelectual, grado de adaptación a un medio,...
- Errores cometidos al medir ciertas magnitudes.
- Valores estadísticos muestrales, por ejemplo: la media.